ROB 201 Calculus for the Modern Engineer
Advert from a student in Fall 2024: Fellow students, when fulfilling your math requirements, you have two pathways to choose from. The first is the traditional route: 12 credits of Calculus courses offered by Michigan’s Math Department, taken over three semesters. This pathway focuses heavily on theory, often without connecting the material to real-world applications in engineering and the sciences.
Read More
The second option is ROB 201: Calculus for the Modern Engineer, a streamlined 4-credit course completed in a single semester. Designed for students in robotics, mechanical engineering, electrical engineering, aerospace engineering, computer science, physics, and naval architecture, ROB 201 focuses on the most critical aspects of calculus while emphasizing practical applications. You’ll not only learn what calculus is but also why it matters and how to use it in solving real-world problems.
Students who take ROB 201 emerge better prepared for upper-level courses in their disciplines, with a stronger foundation in applied math. Taught by a professor with extensive experience in engineering and applied mathematics, this course ensures a meaningful, efficient, and practical calculus education.
The choice is clear: ROB 201 offers a modern, application-focused approach to calculus that’s perfect for today’s engineers and scientists.
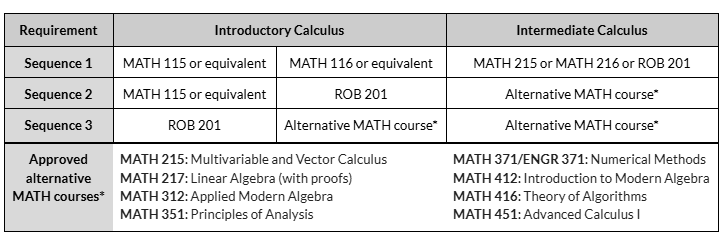
Available Pathways for Robotics Majors: For AY 2025-26, any pathway other than Sequence 1 requires a petition (that will be approved for Robotics majors). This extra step is imposed by the College of Engineering’s Curriculum Committee and not the Robotics Faculty. We apologise for this inconvenience. If you need help, reach out to Robotics Student Services. Non-Robotics Majors or double-majors need to consult with their advisor.
How three semesters to one was accomplished: I condensed Calculus I, Calculus II, and Ordinary Differential Equations into a single 4-credit semester course by building it around three major projects: numerical integration, constrained optimization, and feedback control of the ROB 311 BallBot. These projects provided a natural structure—giving the course a clear beginning, middle, and end—while also ensuring that students engaged deeply with fundamental mathematical concepts in a practical, application-driven way.
Read More
Rather than following the traditional calculus sequence, I deconstructed the subject and rebuilt it from the ground up, rearranging topics to improve conceptual flow. Instead of starting with derivatives, I introduced students to numerical integration first, leveraging their intuitive understanding of summation (I thank Prof. Chad Jenkins for this idea). Antiderivative rules were separated into a distinct chapter, reducing the frustration of manual symbolic integration. This restructuring allowed calculus to unfold in a way that aligned with how students naturally think about and use mathematics in engineering applications.
To make the subject more engaging and relevant, I shifted the emphasis from manual computation to computational problem-solving. By integrating software tools, students could visualize mathematical concepts and experiment with them interactively. Jupyter notebooks played a crucial role in this transformation, allowing homework assignments to combine explanatory text with executable code. This approach harnessed students' intrinsic motivation—when their code produces meaningful results, they are more willing to engage with the underlying mathematical theory.
I also identified natural synergies across topics. For example, numerically evaluating an integral and solving an ODE share the same computational framework. By introducing numerical integration early, I prepared students for ODEs without them realizing it. Similarly, my second project, which uses constrained gradient descent to model a 3-meter platform diver’s motion, is actually an ODE problem in disguise. Students are solving for trajectories without explicitly confronting the underlying differential equations, making the eventual transition to ODEs much smoother. This deliberate layering of concepts ensured that students were ready for ODEs by the time they formally encountered them.
By prioritizing real-world applications, computational exploration, and a logical restructuring of topics, I created a course that not only condenses three traditional courses into one but also makes calculus more intuitive, engaging, and effective for engineering students.
Additional Resources
Course GitHub Site Contains lecture recordings, lecture notes, and HW sets.
PDF of Textbook Calculus for the Modern Engineer by Prof. Jessy Grizzle
Teaching Evaluations Raw data, no editing
Article on ROB 201 (Extended version of ASEE June 2025) Calculus for the Modern Engineer: Putting the Joy Back in Learning Advanced Mathematics
Extracted Slides from a Presentation to CoE UG Chairs Relation of ROB 201 to Math 115, 116, and 216 (Calc I, Calc II, and ODEs), Project Descriptions, and more.
More petitions: Change comes with great difficulty. ROB 201 is not yet officially listed as an accepted prerequisite for the following courses: AEROSP 201, 205, 215; BIOMEDE 211, 231, 517; EECS 203, 215; IOE 265, 366; and MECHENG 240. Robotics is actively working with AERO, BME, IOE, EECS, and ME to formalize these updates. Robotics Student Services can help you with the petition process.
Suggested Paths Through Math Courses for Robotics Students compliments of Prof. Hanna Bennett, Associate Chair for the Undergraduate Program, Mathematics Department, University of Michigan, Ann Arbor.
Course Flyer Course description, teaching evaluations, article on the course, grades from the pilot semester in Fall 2024, FAQs, such as who can take the course and how does it count for credit.
Contents Topic Coverage Organized by the Traditional Curriculum; distinct from the book’s internal organization.

